配列のインデックスアクセス#
前の紹介で、多次元配列に対するインデックスアクセスの方法をいくつかの例を通して紹介しました。実際にNumPyが提供するインデックス機能は非常に強力で、読者が「ブロードキャスト」に関する知識を習得した後、配列のインデックスルールを体系的に学び直しましょう。
import numpy as np
import helper.magics
インデックスオブジェクト#
まず、多次元配列のインデックスは、配列の次元数と同じ長さのタプルであるべきです。インデックスタプルの長さが配列の次元数より大きい場合はエラーとなり、小さい場合は不足分に「:」を補い、配列の次元数と揃えます。
インデックスオブジェクトがタプルでない場合、NumPy はそれを単一要素のタプルとして扱います。様々な変換や「:」の追加を経て、標準的なインデックスタプルが得られます。このタプルの各要素には、スライス、整数、整数配列、ブール配列などのタイプがあります。これら以外の要素、例えばリストやタプルは、整数配列に変換されます。
例えば、三次元配列 a に対して、二次元リスト lidx と、それを tuple に変換した tidx をインデックスとして使用すると、異なる結果が得られます。これは、NumPy がリスト lidx を (lidx, :, :) と解釈するのに対し、tidx は (tidx[0], tidx[1], :) として扱われるためです。
a = np.arange(3 * 4 * 5).reshape(3, 4, 5)
lidx = [[0], [1]]
tidx = tuple(lidx)
%C a[lidx]; a[tidx]
a[lidx] a[tidx]
-------------------------- -----------------
[[[[ 0, 1, 2, 3, 4], [[5, 6, 7, 8, 9]]
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]]],
[[[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29],
[30, 31, 32, 33, 34],
[35, 36, 37, 38, 39]]]]
インデックスタプルのすべての要素がスライスと整数である場合、それをインデックスとして使用すると、元の配列のビューが得られます。つまり、元の配列とデータストレージを共有します。
整数配列をインデックスとして使用#
次に、インデックスタプルの要素がスライスと整数配列で構成されている場合を見てみましょう。整数配列が\(N_t\)個あり、スライスが\(N_s\)個あるとします。\(N_t+N_s\)は配列の次元数\(D\)です。
まず、これらの\(N_t\)個の整数配列はブロードキャスト条件を満たす必要があります。それらがブロードキャストされた後の次元数を\(M\)とし、その形状を\((d_0, d_1, ..., d_{M-1})\)とします。
\(N_s\)が0、つまりスライス要素がない場合、インデックスによって得られる結果配列resultの形状は、整数配列がブロードキャストされた後の形状と同じです。その各要素の値は以下の式で得られます:
ここで、\(ind_0\)から\(ind_{N_t-1}\)はブロードキャストされた整数配列です。この式を理解するために、例を見てみましょう:
Tip
指定された軸に沿って整数配列を使用して要素を取得するだけであれば、numpy.take()関数を使用できます。この関数は整数配列のインデックス演算よりも少し速く、インデックス越界処理もサポートしています。
i0 = np.array([[1, 2, 1], [0, 1, 0]])
i1 = np.array([[[0]], [[1]]])
i2 = np.array([[[2, 3, 2]]])
b = a[i0, i1, i2]
b
array([[[22, 43, 22],
[ 2, 23, 2]],
[[27, 48, 27],
[ 7, 28, 7]]])
まず、i0、i1、i2の3つの整数配列のshape属性はそれぞれ(2,3)、(2,1,1)、(1,1,3)です。ブロードキャストルールに従い、長さが3未満のshape属性の前に1を補い、それらの次元数を同じにします。ブロードキャスト後のshape属性は各軸の最大値になります:
(1, 2, 3)
(2, 1, 1)
(1, 1, 3)
---------
2 2 3
つまり、3つの整数配列がブロードキャストされた後のshape属性は(2,2,3)であり、これがインデックス演算によって得られる結果配列の次元数です:
b.shape
(2, 2, 3)
broadcast_arrays()を使用してブロードキャスト後の配列を確認できます:
ind0, ind1, ind2 = np.broadcast_arrays(i0, i1, i2)
%C ind0; ind1; ind2
ind0 ind1 ind2
------------- ------------- -------------
[[[1, 2, 1], [[[0, 0, 0], [[[2, 3, 2],
[0, 1, 0]], [0, 0, 0]], [2, 3, 2]],
[[1, 2, 1], [[1, 1, 1], [[2, 3, 2],
[0, 1, 0]]] [1, 1, 1]]] [2, 3, 2]]]
bの任意の要素b[i,j,k]は、配列aのind0、ind1、ind2によるインデックス変換後の値です:
i, j, k = 0, 1, 2
print(b[i, j, k], a[ind0[i, j, k], ind1[i, j, k], ind2[i, j, k]])
i, j, k = 1, 1, 1
print(b[i, j, k], a[ind0[i, j, k], ind1[i, j, k], ind2[i, j, k]])
2 2
28 28
次に、\(N_s\)が0でない場合を考えます。スライスインデックスが存在する場合、状況はさらに複雑になります。以下の2つのケースに細分化できます:インデックスタプル内の整数配列間にスライスがない場合、つまり整数配列が1つだけまたは連続した複数の整数配列である場合。この場合、結果配列のshape属性は、元の配列のshape属性のうち整数配列が占める部分をそれらがブロードキャストされた後のshape属性に置き換えたものになります。例えば、元の配列aのshape属性が(3,4,5)で、i0とi1がブロードキャストされた後の形状が(2,2,3)である場合、a[1:3,i0,i1]の形状は(2,2,2,3)になります:
c = a[1:3, i0, i1]
c.shape
(2, 2, 2, 3)
ここで、cのshape属性の最初の2はスライス「1:3」の長さで、後ろの(2,2,3)はi0とi1がブロードキャストされた後の配列の形状です:
ind0, ind1 = np.broadcast_arrays(i0, i1)
ind0.shape
(2, 2, 3)
i, j, k = 1, 1, 2
print(c[:, i, j, k])
print(a[1:3, ind0[i, j, k], ind1[i, j, k]]) # c[:,i,j,k]と同じ値
[21 41]
[21 41]
インデックスタプル内の整数配列が連続していない場合、結果配列のshape属性は整数配列がブロードキャストされた後の形状にスライス要素に対応する形状を追加したものになります。例えば、a[i0,:,i1]のshape属性は(2,2,3,4)です。ここで、(2,2,3)はi0とi1がブロードキャストされた後の形状で、4は配列aの第1軸の長さです:
d = a[i0, :, i1]
d.shape
(2, 2, 3, 4)
i, j, k = 1, 1, 2
%C d[i,j,k,:]; a[ind0[i,j,k],:,ind1[i,j,k]]
d[i,j,k,:] a[ind0[i,j,k],:,ind1[i,j,k]]
---------------- ----------------------------
[ 1, 6, 11, 16] [ 1, 6, 11, 16]
複雑な例#
次に、学んだインデックスアクセスの知識を使って、NumPyメーリングリストで提起された比較的古典的な問題を解決しましょう。
問題を少し簡略化します。質問者が実現したいインデックス演算は次の通りです:形状が(I, J, K)の三次元配列vと形状が(I, J)の二次元配列idxがあり、idxの各値は0からK-Lの整数です。彼はインデックス演算を通じて配列rを得たいと考えており、第0軸と第1軸の各インデックスiとjに対して次の条件を満たします:
r[i,j,:] = v[i,j,idx[i,j]:idx[i,j]+L]
次のグラフに示すように、左図の不透明なブロックが取得したい部分で、インデックス演算後に右図のような配列が得られます。
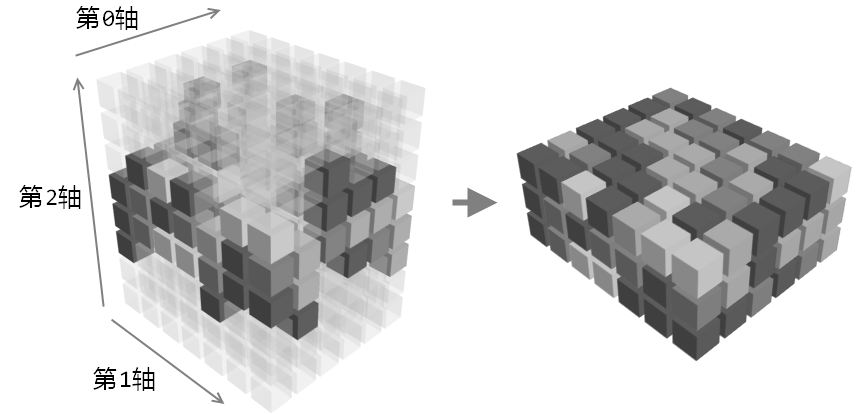
まず、デバッグに便利な配列vを作成します。これは第2軸の各層の値がその層の高さ、つまりv[:,:,i]のすべての要素の値がiです。次に、配列idxをランダムに生成します。その各要素の値は0からK-Lの間です:
I, J, K, L = 6, 7, 8, 3
_, _, v = np.mgrid[:I, :J, :K]
idx = np.random.randint(0, K - L, size=(I, J))
次に、配列idxを使用して第2軸のインデックス配列idx_kを作成します。これは形状が(I,J,L)の三次元配列です。その第2軸の各層の値はidx配列に層の高さを加えたもの、つまりidx_k[:,:,i] = idx_k[:,:]+iです:
idx_k = idx.reshape(I, J, 1) + np.arange(3)
idx_k.shape
(6, 7, 3)
次に、第0軸と第1軸のインデックス配列を作成します。それらのshapeはそれぞれ(I,1,1)と(1,J,1)です:
idx_i, idx_j, _ = np.ogrid[:I, :J, :K]
idx_i, idx_j, idx_kを使用して配列vにインデックス演算を行うことで結果を得ます:
r = v[idx_i, idx_j, idx_k]
i, j = (
2,
3,
) # 結果を検証します。読者はこれをループを使用してすべての要素を検証するように変更できます
%C r[i,j,:]; v[i,j,idx[i,j]:idx[i,j]+L]
r[i,j,:] v[i,j,idx[i,j]:idx[i,j]+L]
--------- --------------------------
[2, 3, 4] [2, 3, 4]
ブール配列をインデックスとして使用#
ブール配列を直接インデックスオブジェクトとして使用する場合、またはタプルインデックスオブジェクトにブール配列が含まれている場合、nonzero()を使用してブール配列を整数配列のグループに変換し、それらの整数配列を使用してインデックス演算を行います。
nonzeros(a)は配列aの値がゼロでない要素のインデックスを返します。その戻り値は長さがa.ndim(配列aの軸数)のタプルで、タプルの各要素は整数配列であり、その値は非ゼロ要素のインデックスが対応する軸上の値です。例えば、一次元ブール配列b1の場合、nonzero(a)によって得られるのは長さ1のタプルで、b1[0]とb1[2]の値が0でないことを示します。
Tip
指定された軸に沿ってブール配列を使用して要素を取得するだけであれば、numpy.compress()関数を使用できます。
b1 = np.array([True, False, True, False])
np.nonzero(b1)
(array([0, 2]),)
二次元配列b2の場合、nonzero(a)によって得られるのは長さ2のタプルです。その第0要素は配列aの値が0でない要素の第0軸のインデックスで、第1要素は第1軸のインデックスです。したがって、以下の結果からb2[0,0], b[0,2], b2[1,0]の値が0でないことがわかります:
b2 = np.array(
[
[True, False, True, False],
[True, False, False, False],
[False, False, False, False],
]
)
np.nonzero(b2)
(array([0, 0, 1]), array([0, 2, 0]))
ブール配列を直接インデックスとして使用する場合、nonzero()によって変換されたタプルをインデックスオブジェクトとして使用するのと同じです:
a = np.arange(3 * 4 * 5).reshape(3, 4, 5)
%C a[b2]; a[np.nonzero(b2)]
a[b2] a[np.nonzero(b2)]
---------------------- ----------------------
[[ 0, 1, 2, 3, 4], [[ 0, 1, 2, 3, 4],
[10, 11, 12, 13, 14], [10, 11, 12, 13, 14],
[20, 21, 22, 23, 24]] [20, 21, 22, 23, 24]]
インデックスオブジェクトがタプルで、その中にブール配列が含まれている場合、ブール配列をnonzeros()によって変換された各整数配列に展開するのと同じです:
b3 = np.array(
[
[True, False, True, False, False],
[True, False, False, False, False],
[False, False, False, False, False],
[False, False, False, False, False],
]
)
%C a[1:3, b3]; a[1:3, np.nonzero(b3)[0], np.nonzero(b3)[1]]
a[1:3, b3] a[1:3, np.nonzero(b3)[0], np.nonzero(b3)[1]]
-------------- --------------------------------------------
[[20, 22, 25], [[20, 22, 25],
[40, 42, 45]] [40, 42, 45]]