巡回セールスマン問題

巡回セールスマン問題#

巡回セールスマン問題とは、複数の都市を訪問し、すべての都市を一度ずつ巡った後、出発地点に戻る最短経路を求める問題です。CP-SATのadd_circuit()とminimize()を併用することで、この問題を解くことができます。本章では、巡回セールスマン問題の概要と、CP-SATを用いた解法について説明します。

巡回セールスマン問題（TSP）の難点は、以下のような点にあります。

計算量の爆発（組み合わせ爆発
- TSPはNP困難（NP-hard）に分類される問題であり、都市の数 ( N ) が増えると、考えられる経路の数は ( (N-1)!/2 ) という指数関数的な増加を示します。
- 例えば、10都市では約18万通り、20都市では約1.2兆通りもの経路が存在し、単純な総当たりでは解くことが困難になります。
最適解を求めるのが難しい
- 近似アルゴリズム（貪欲法、局所探索、遺伝的アルゴリズムなど）を使えば高速に解が得られますが、必ずしも最適解とは限りません。
- 厳密解を求めるには、整数線形計画法（MILP）、分枝限定法、動的計画法（Held-Karpアルゴリズム）などの高度な手法が必要ですが、都市数が増えると計算コストが急激に増加します。

from matplotlib import pyplot as plt
import numpy as np
from scipy import spatial
from matplotlib.collections import LineCollection
from ortools.sat.python import cp_model

テストデータ#

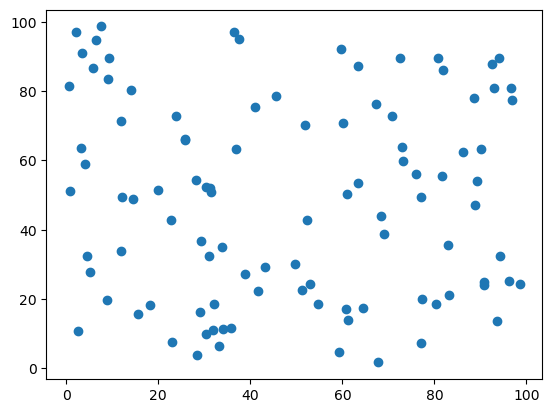
次のコードでは、ランダムに100点の座標を生成し、それらの点間の距離行列を計算します。CP-SATは整数のみを扱うため、距離を1000倍して整数に変換します。

n = 100
np.random.seed(42)
points = np.random.uniform(0, 100, size=(n, 2))
dist_matrix = (spatial.distance.squareform(spatial.distance.pdist(points)) * 1000).astype(np.int32)
fig, ax = plt.subplots()
ax.scatter(points[:, 0], points[:, 1]);

_images/993b7013bd88eef781a7b6fbc7c5bdb849e95bf2b1e64c8b555886d13577d8ff.png

TSP問題を解くコード#

次の ObjectiveTracker は、CpSolverSolutionCallback を継承したコールバッククラスで、最適化の途中経過（目的関数の履歴）を記録するためのものです。self.history に self.objective_value（現在の目的関数値）を追加することで、解がどのように改善されていくかを追跡できます。

class ObjectiveTracker(cp_model.CpSolverSolutionCallback):
    def __init__(self):
        super().__init__()
        self.history = []

    def on_solution_callback(self):
        self.history.append(self.objective_value)

次の solve_points_tsp() 関数は、実際に TSP 問題を解くものです。引数は以下のとおりです。

points：都市（座標）のリスト
dist_matrix：都市間の距離行列
log_history：True の場合、探索履歴を記録
max_time：ソルバーの最大実行時間（秒）

TSP 問題を解くには、まず dist_matrix を (i, j) のキーに変換し、辞書 edges に格納します。i != j の条件により、同じ都市への自己ループは除外されます。これにより、都市間のエッジの重み（距離）を記録できます。

次に、各エッジ (i, j) に対して、対応する 0 または 1 のブール変数を作成します。解として True が選択された場合、そのエッジが巡回路に含まれることを意味します。

add_circuit() を使用すると、1 つの閉じた巡回路になるように制約が追加され、すべての都市を 1 回だけ訪問し、最終的に出発点に戻るようになります。LinearExpr.weighted_sum() を用いて、選択されたエッジの合計距離を計算し、model.minimize(length) によって、この合計距離が最小となるよう最適化を行います。

def solve_points_tsp(points, dist_matrix, log_history=False, max_time=10):
    edges = {}
    for (i, j), d in np.ndenumerate(dist_matrix):
        if i != j:
            edges[i, j] = int(d)

    model = cp_model.CpModel()
    variables = {key:model.new_bool_var(f'{i}') for i, key in enumerate(edges)}
    model.add_circuit([(s, e, v) for (s, e), v in variables.items()])
    length = cp_model.LinearExpr.weighted_sum(list(variables.values()), list(edges.values()))
    model.minimize(length)
    solver = cp_model.CpSolver()
    solver.parameters.max_time_in_seconds = max_time
    if log_history:
        callback = ObjectiveTracker()
        status = solver.solve(model, callback)
        print(callback.history)
    else:
        status = solver.solve(model)
    
    selected_edges = points[np.array([key for key, v in variables.items() if solver.value(v)])]
    return selected_edges

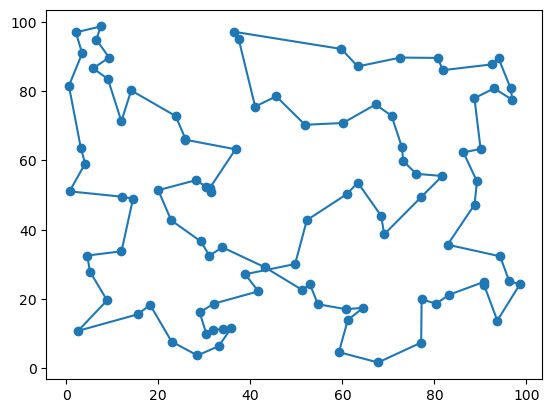
次に、100 点のランダムな座標について TSP を解いてみます。

selected_edges = solve_points_tsp(points, dist_matrix, log_history=True)
fig, ax = plt.subplots()
ax.scatter(points[:, 0], points[:, 1])
ax.add_collection(LineCollection(selected_edges));

[4269157.0, 1128682.0, 1077553.0, 1070650.0, 1068858.0, 1064624.0, 1046599.0, 778747.0, 761230.0]

_images/74d337bca69aa152dbfe08ffcb2a127106f53c276246f8f41fef1b49a5619bf6.png

線分の TSP 問題#

作成したブール変数に追加の制約を加えることで、さまざまな特殊な TSP 問題を解くことができます。たとえば、次の問題では50 本の線分を巡回する最適なルートを求めます。次のコードでは、各線分の始点 (start_points) と終点 (end_points) をランダムに生成し、TSP の対象とします。

n = 50
np.random.seed(42)
start_points = np.random.uniform(0, 100, size=(n, 2))
length = np.random.uniform(5, 10, size=n)
angle = np.random.uniform(0, 2 * np.pi, size=n)
end_points = start_points + np.c_[length * np.cos(angle), length * np.sin(angle)]
segments = np.column_stack([start_points, end_points])
points = segments.reshape(-1, 2)
fig, ax = plt.subplots()
ax.scatter(start_points[:, 0], start_points[:, 1])
ax.scatter(end_points[:, 0], end_points[:, 1])
ax.add_collection(LineCollection(segments.reshape(-1, 2, 2)))

<matplotlib.collections.LineCollection at 0x25d8e4aa030>

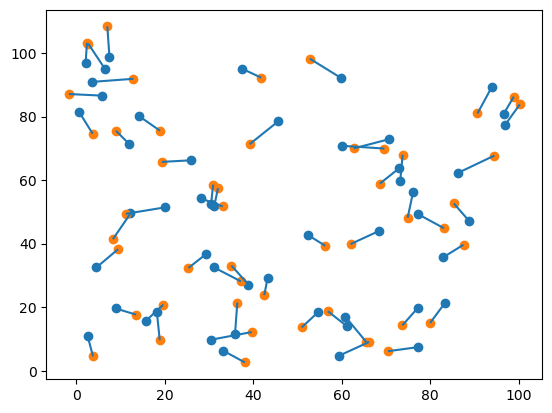
_images/74a3f55dc1ce740fe3581d42bf400dad295765d54708d8a64285addb0038d201.png

次のコードでは、同じ線分の端点間の距離を 0 に設定し、solve_points_tsp() を使用して解いてみましたが、解はすべての線分（赤色）を通っていません。その理由は、同じ線分の端点間のコストは 0 になりますが、それでも巡回路全体の長さを最小化しようとするため、すべての線分を経由するとは限りません。

dist_matrix = (spatial.distance.squareform(spatial.distance.pdist(segments.reshape(-1, 2))) * 1000).astype(np.int32)
start_index = np.arange(0, n*2, 2)
end_index = start_index + 1
dist_matrix[start_index, end_index] = 0
dist_matrix[end_index, start_index] = 0

selected_edges = solve_points_tsp(points, dist_matrix, log_history=True)
fig, ax = plt.subplots()
ax.scatter(start_points[:, 0], start_points[:, 1])
ax.scatter(end_points[:, 0], end_points[:, 1])
ax.add_collection(LineCollection(segments.reshape(-1, 2, 2), linewidth=5, color='red', alpha=0.6))
ax.add_collection(LineCollection(selected_edges, linewidth=2))

[4720978.0, 947648.0, 930508.0, 845542.0, 828402.0, 809087.0, 482796.0]

<matplotlib.collections.LineCollection at 0x25d8d4822d0>

_images/fdc2b01007814f12955fc54914b9257ec5b7dc4931626fb44bebbc9726e4f2a7.png

次のコードでは、同じ線分の端点 s と e に対して、辺 (s, e) と (e, s) に対応するブール変数の一方が必ず True になるように制約を追加し、すべての線分を通る制約を加えています。これで、solve_segments_tsp() 関数がすべての線分を通る巡回ルートを最適化します。

def solve_segments_tsp(points, dist_matrix, log_history=False, max_time=10):
    edges = {}
    for (i, j), d in np.ndenumerate(dist_matrix):
        if i != j:
            edges[i, j] = int(d)

    n = dist_matrix.shape[0]
    start_index = np.arange(0, n, 2)
    end_index = start_index + 1

    model = cp_model.CpModel()
    variables = {key:model.new_bool_var(f'{i}') for i, key in enumerate(edges)}
    model.add_circuit([(s, e, v) for (s, e), v in variables.items()])
    
    for s, e in zip(start_index, end_index):
        model.add_exactly_one([variables[s, e], variables[e, s]])
    
    length = cp_model.LinearExpr.weighted_sum(list(variables.values()), list(edges.values()))
    model.minimize(length)
    solver = cp_model.CpSolver()
    solver.parameters.max_time_in_seconds = max_time
    if log_history:
        callback = ObjectiveTracker()
        status = solver.solve(model, callback)
        print(callback.history)
    else:
        status = solver.solve(model)
    
    selected_edges = points[np.array([key for key, v in variables.items() if solver.value(v)])]
    return selected_edges

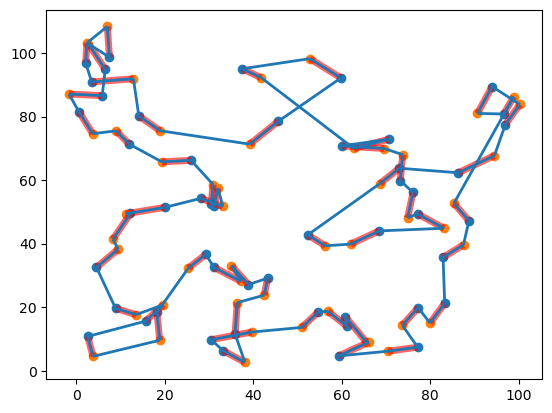
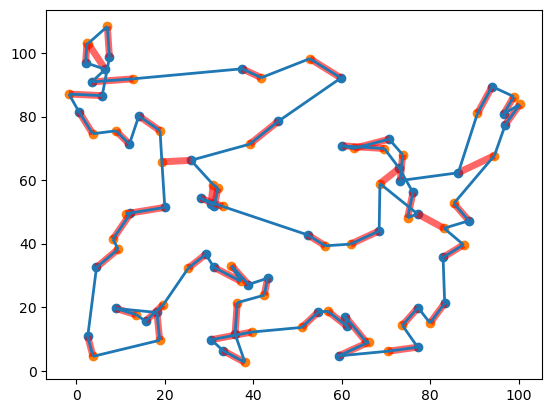
次に、線分の TSP 問題を解いてみます。結果からわかるように、ルートはすべての線分を通っています。このコードでは、solve_segments_tsp() 関数で求めた最適な巡回ルートをプロットしています。赤色で示された線分が元々の線分で、選ばれた巡回ルート（最適な経路）が別の色で表示されます。

selected_edges = solve_segments_tsp(points, dist_matrix, log_history=True)
fig, ax = plt.subplots()
ax.scatter(start_points[:, 0], start_points[:, 1])
ax.scatter(end_points[:, 0], end_points[:, 1])
ax.add_collection(LineCollection(segments.reshape(-1, 2, 2), linewidth=5, color='red', alpha=0.6))
ax.add_collection(LineCollection(selected_edges, linewidth=2))

[873781.0, 733917.0, 720673.0, 700814.0, 623658.0, 544530.0, 543938.0, 527675.0, 527083.0, 482358.0, 480641.0]

<matplotlib.collections.LineCollection at 0x25d9553b680>

_images/4c073877346958fda890f9f68d6c7049798c3691e7cfb477a96fb80f2a5eae41.png

巡回セールスマン問題

Contents

巡回セールスマン問題#

テストデータ#

TSP問題を解くコード#

線分の TSP 問題#