スリザーリンク#
スリザーリンク(Slitherlink)は、方眼状の盤面に配置された数字をヒントにして、線を引いて一つの閉じたループを作るパズルです。以下に基本ルールを説明します。
スリザーリンクパズルのサイト
helper.puzzle.extract_slither_link() を使うと、このサイトのパズル盤面を取得できます。ブラウザの開発者ツールを開き、盤面を表す <div> タグのコードをコピーし、この関数を実行すると、盤面が配列として取得できます。
線を引く
・盤面の点(格子点)を結ぶように、縦または横に線を引くことができます。
・線は途中で途切れたり、交差したり、枝分かれしたりしてはいけません。数字の意味
・マスに書かれた数字は、そのマスの周囲に引かれる線の本数を表します。
・例えば「3」が書かれたマスの周囲には、必ず3本の線が引かれます。
・「0」のマスの周囲には線を引いてはいけません。
・数字が書かれていないマスは、線の本数に制限がありません。閉じたループを作る
・すべての線はつながり、一つの閉じたループ(輪)を形成しなければなりません。
・ループは枝分かれや交差をしてはいけません。
盤面上の点を頂点とし、ループの横線または縦線を辺とすることで、スリザーリンクは回路を探索する問題となります。そのため、CP-SATのadd_circuit()制約を使用して解くことができます。 また、すべての頂点を通る必要がないため、特定の頂点を除外できるように、すべての頂点に対して(i, i, bool_var)の辺をadd_circuit()に追加します。
from ortools.sat.python import cp_model
import numpy as np
from matplotlib import pyplot as plt
from collections import defaultdict
盤面の読み込みと描画#
次のコードで盤面を読み込み、描画します。
from matplotlib.collections import LineCollection
def plot_slither_link_board(board, result=None):
h, w = board.shape
fig, ax = plt.subplots(figsize=(w*0.3, h*0.3))
ax.set_ylim(-0.1, h + 0.1)
ax.set_xlim(-0.1, w + 0.1)
ax.invert_yaxis()
ax.set_aspect("equal")
all_segments = []
circuit_segments = []
if result is not None:
for (n1, n2), flag in result.items():
if flag:
r1, c1 = n1 // (w + 1), n1 % (w + 1)
r2, c2 = n2 // (w + 1), n2 % (w + 1)
circuit_segments.append([(c1, r1), (c2, r2)])
for r, c in np.ndindex(h + 1, w + 1):
if r + 1 <= h:
all_segments.append([(c, r), (c, r + 1)])
if c + 1 <= w:
all_segments.append([(c, r), (c + 1, r)])
ax.add_collection(LineCollection(all_segments, color='gray', alpha=0.5))
ax.add_collection(LineCollection(circuit_segments, color='green', linewidth=2))
for (i, j), v in np.ndenumerate(board):
if v != -1:
ax.text(j + 0.5, i + 0.5, str(v), fontsize=12, va='center', ha='center')
ax.autoscale_view()
ax.axis('off')
return fig, ax
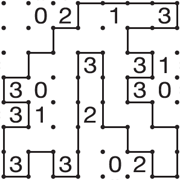
board = np.loadtxt('data/slitherlink01.txt', dtype=np.int8)
plot_slither_link_board(board);
解くコード#
次のコードは、スリザーリンクパズルを解くクラス SlitherLinkSolver を定義しています。
class SlitherLinkSolver:
def __init__(self, board):
self.board = board
h, w = self.board.shape
self.nodes = nodes = np.arange((h + 1) * (w + 1)).reshape(h + 1, w + 1)
self.edges = edges = []
for (r, c), s in np.ndenumerate(nodes):
if c + 1 <= w:
right = (r, c + 1)
e = nodes[right]
edges.extend([(s, e), (e, s)])
if r + 1 <= h:
below = (r + 1, c)
e = nodes[below]
edges.extend([(s, e), (e, s)])
self.cell_edges = cell_edges = defaultdict(set)
for (r, c), _ in np.ndenumerate(board):
n1 = nodes[r, c]
n2 = nodes[r, c + 1]
n3 = nodes[r + 1, c]
n4 = nodes[r + 1, c + 1]
for edge in [(n1, n2), (n1, n3), (n2, n4), (n3, n4)]:
cell_edges[r, c].add(edge)
cell_edges[r, c].add(edge[::-1])
model = cp_model.CpModel()
variables = {e:model.new_bool_var(f'edge{e}') for e in edges}
dummies = [(i, i, model.new_bool_var(f'dummy_{i}')) for i in range(0, (h + 1) * (w + 1))]
model.add_circuit([(s, e, v) for (s, e), v in variables.items()] + dummies)
for (r, c), count in np.ndenumerate(board):
box_edges = [variables[edge] for edge in cell_edges[r, c]]
if count != -1:
model.add(sum(box_edges) == count)
solver = cp_model.CpSolver()
solver.solve(model)
self.result = {key:solver.value(val) for key, val in variables.items()}
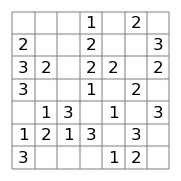
solver = SlitherLinkSolver(board)
plot_slither_link_board(board, solver.result);
コードの説明#
h × w の盤面の場合、(h+1) × (w+1) の格子点が存在します。各格子点を 1 次元の整数インデックスで管理し、形状 (h+1, w+1) の NumPy 配列 nodes に格納します。これにより、各ノードに固有の ID を割り当てることができます。
self.nodes = nodes = np.arange((h + 1) * (w + 1)).reshape(h + 1, w + 1)
次に、各ノード (r, c) について、右 (r, c+1) および下 (r+1, c) に隣接するノードとの間に双方向の辺 (s, e), (e, s) を追加します。これにより、ループを形成するためのすべての候補となる線が self.edges に格納されます。
self.edges = edges = []
for (r, c), s in np.ndenumerate(nodes):
if c + 1 <= w:
right = (r, c + 1)
e = nodes[right]
edges.extend([(s, e), (e, s)])
if r + 1 <= h:
below = (r + 1, c)
e = nodes[below]
edges.extend([(s, e), (e, s)])
次に、各セル (r, c) について、そのセルを構成する 4 本の辺(合計 8 つの有向辺)を cell_edges[r, c] に格納します。
self.cell_edges = cell_edges = defaultdict(set)
for (r, c), _ in np.ndenumerate(board):
n1 = nodes[r, c]
n2 = nodes[r, c + 1]
n3 = nodes[r + 1, c]
n4 = nodes[r + 1, c + 1]
for edge in [(n1, n2), (n1, n3), (n2, n4), (n3, n4)]:
cell_edges[r, c].add(edge)
cell_edges[r, c].add(edge[::-1])
各辺に対応するブール変数を作成します。
model = cp_model.CpModel()
variables = {e: model.new_bool_var(f'edge{e}') for e in edges}
add_circuit() は回路制約を追加し、1 つの閉じたループを強制します。ただし、スリザーリンクではすべてのノードを通る必要がないため、(i, i, bool_var) の自己ループ(ダミー辺)を作成し、add_circuit() に追加します。この自己ループを利用することで、ループに含まれないノードを表現し、部分的な回路の除外を可能にします。
dummies = [(i, i, model.new_bool_var(f'dummy_{i}')) for i in range((h + 1) * (w + 1))]
model.add_circuit([(s, e, v) for (s, e), v in variables.items()] + dummies)
最後に、セルごとの辺の制約を追加します。マスに書かれた数字 count が -1 でない場合、そのマスの周囲の線の本数が count になるように制約を追加します。
for (r, c), count in np.ndenumerate(board):
box_edges = [variables[edge] for edge in cell_edges[r, c]]
if count != -1:
model.add(sum(box_edges) == count)
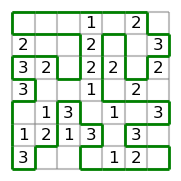
最も難しいパズル#
最後に、最も難しいパズルを解いてみます。
board = np.loadtxt('data/slitherlink02.txt', dtype=np.int8)
solver = SlitherLinkSolver(board)
plot_slither_link_board(board, solver.result);
