ナンバーリンクパズル

ナンバーリンクは、指定された数のペアを「途切れずに」線で結ぶパズルです。基本的なルールは以下のとおりです。

See also

OrToolsでナンバーリンクパズルを解く

盤面

• 盤面は格子状（グリッド状）のマス目で構成されています。

• いくつかのマスには数字が書かれています。

• 盤面のサイズは自由ですが、例えば10×10の盤面などが一般的です。

目標

• 同じ数字が書かれた 2つのマスを線でつなぐことが目的です。

• すべての数字のペアを正しくつなげればクリアとなります。

線のルール

• 線は上下左右にのみ進むことができます。（斜めは禁止）

• 他の線と交差したり、枝分かれしたりしてはいけません。

• すべてのマスを埋める必要はありません。マスが空白のままでもOK）

クリア条件
以下の条件を満たせばクリアです：
✅ すべての数字のペアが線でつながっている
✅ 線が交差せず、分岐もない
✅ すべての線が連続している（途切れがない）

ナンバーリンクパズルのサイト

https://puzzlemadness.co.uk/numberlink/medium

helper.puzzle.extract_number_link() を使うと、このサイトのパズル盤面を取得できます。ブラウザのソースコードを開き、puzzledata の行にある JSON データをコピーしてこの関数を実行すると、盤面が配列として返されます。

盤面の定義

本書が処理するナンバーリンクパズルの盤面は、以下のような2次元配列によって定義します。。

• 0は空白のマスを表し、どの数字にも属していません。

• その他の数値（1以上の整数）はペアとなる数字を表し、対応する2つのマスを線で結ぶ必要があります。

import numpy as np
board = np.loadtxt('data/numberlink01.txt', dtype=np.uint8)
print(board)

[[1 0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 5 0]
 [0 6 0 1 0 0 0 0 0 0]
 [0 0 0 0 0 4 3 0 0 0]
 [0 0 0 0 0 0 6 0 5 0]
 [0 8 0 3 0 0 0 0 0 0]
 [0 0 0 4 7 0 0 0 0 0]
 [0 0 0 0 0 0 2 0 8 0]
 [0 7 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 2]]

次の plot_board() は、盤面 board とその解 links を描画します。links は辞書型で、キーは (r1, c1, r2, c2) の形式のタプル、値は Bool 値です。値が True の場合、マス (r1, c1) と (r2, c2) がつながっていることを意味します。cellsはマス(r, c)の数値を保存する辞書です。

from matplotlib import pyplot as plt
from matplotlib.cm import tab20

def plot_number_link_board(board, links=None, cells=None):
    h, w = board.shape
    fig, ax = plt.subplots(1, 1, figsize=(w * 0.4, h * 0.4))
    if links is not None and cells is not None:
        for (r1, c1, r2, c2), link in links.items():
            if link:
                ax.plot([c1, c2], [r1, r2], color=tab20.colors[cells[r1, c1]], lw=3)
    xs = []
    ys = []
    texts = []
    for (r, c), v in np.ndenumerate(board):
        xs.append(c)
        ys.append(r)
        texts.append(str(v))
    
    ax.scatter(xs, ys)
    for x, y, s in zip(xs, ys, texts):
        if s != "0":
            ax.text(x, y, s, ha='center', va='center', fontsize=12, 
                    bbox=dict(facecolor=tab20.colors[int(s)], edgecolor='black', boxstyle='round,pad=0.2'))
    
    ax.invert_yaxis()
    ax.axis('off')
    return fig

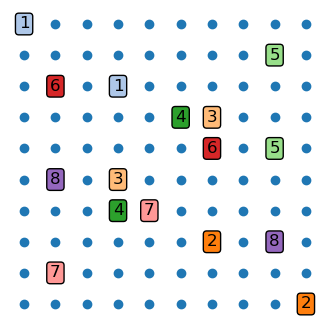
plot_number_link_board(board);

解を探すコード

次のコードで解を求めます。

• cells は、各マス (r, c) の数値を表す変数の辞書です。

• links は、前述の links と同じ形式の辞書で、値は Z3 の Bool 型の変数です。

• cell_links は、各マス (r, c) に関連する link を保持する辞書です。

制約条件は以下のようです。

1. 各マスの数値は0以上かつ最大値以下でなければならない。

2. 元々数値があるマスでは、その数値を変更しない。

3. 元々数値があるマスの周囲のリンクには1つだけTrueがあり、その数値がルートの端点を表す。

4. 元々空白のマスの周囲のリンクにはちょうど2つのTrueがあり、ルートがこのマスを通ることを意味する。

5. リンクがTrueの場合、リンクされた2つのマスの数値は等しくなければならない。

from z3 import *
from collections import defaultdict

def solve_number_link(board):
    h, w = board.shape
    max_value = board.max()
    
    cells = {}
    links = {}
    cell_links = defaultdict(set)
    
    for (r, c), v in np.ndenumerate(board):
        cells[r, c] = Int(f"C_{r}_{c}")
        r2, c2 = r, c + 1
        if c2 < w:
            links[r, c, r2, c2] = v = Bool(f"L_{r}_{c}_{r2}_{c2}")
            cell_links[r, c].add(v)
            cell_links[r2, c2].add(v)
            
        r2, c2 = r + 1, c
        if r2 < h:
            links[r, c, r2, c2] = v = Bool(f"L_{r}_{c}_{r2}_{c2}")
            cell_links[r, c].add(v)
            cell_links[r2, c2].add(v)
    
    s = Solver()
    
    # 各マスの数値の範囲制約
    for cell in cells.values():
        s.add(0 <= cell, cell <= max_value)
    
    for (r, c), v in np.ndenumerate(board):
        if v > 0:
            # 元々数値があるマスでは、その数値を変更しない
            s.add(cells[r, c] == v) 
            # 元々数値があるマスの周囲のリンクには1つだけTrue
            s.add(PbEq([(b, 1) for b in cell_links[r, c]], 1))
        else:
            # 元々空白のマスの周囲のリンクにはちょうど2つのTrue
            s.add(PbEq([(b, 1) for b in cell_links[r, c]], 2))
    
    # リンクがある場合、マスの数値は等しくする
    for (r, c, r2, c2), b in links.items():
        s.add(Implies(b, cells[r, c] == cells[r2, c2]))
    
    s.check()
    model = s.model()
    links = {key:model[val] for key, val in links.items()} 
    cells = {key:model[val].as_long() for key, val in cells.items()}
    return links, cells

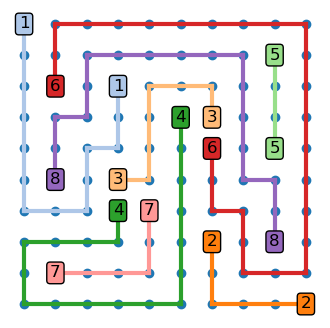
board = np.loadtxt('data/numberlink01.txt', dtype=np.uint8)
links, cells = solve_number_link(board)
plot_number_link_board(board, links, cells);

複雑なパズル

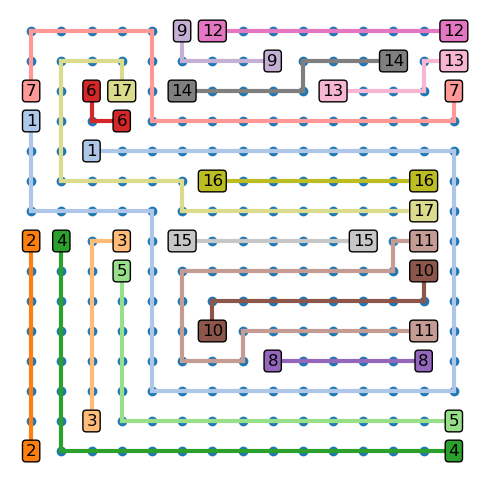
次は複雑なパズルに挑戦してみます。

%%time
board = np.loadtxt('data/numberlink02.txt', dtype=np.uint8)
links, cells = solve_number_link(board)
plot_number_link_board(board, links, cells);

CPU times: total: 1.11 s
Wall time: 1.18 s