箱詰めパズル#
12種類の両面ペントミノを特定の形の箱に詰めるパズルです。CP-SATなどのソルバーを使用すれば、簡単に解くことができます。必要な制約条件は add_exactly_one() だけです。本章では、箱詰めパズルの解き方を説明します。
from ortools.sat.python import cp_model
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.cm import tab20
from matplotlib.collections import PatchCollection
ペントミノのリスト#
ペントミノは、位数5のポリオミノです。同じ大きさの正方形を5つ、辺に沿ってつなげた形を指します。回転や鏡映の操作によって同じ形とみなされるものをまとめると、全部で12種類ございます。これらを総称して「ペントミノ」と呼びます。
次のプログラムは、12種類のペントミノを定義し、それらを同じグラフ上に並べて表示します。
pentominos = dict(
F=[" **", # F
"** ",
" * "],
P=["***", # P
"** "],
I=["*****"], # I
N=["** ", # N
" ***"],
L=["****", # L
" *"],
T=["***", # T
" * ",
" * "],
U=["* *", # U
"***"],
V=["* ", # V
"* ",
"***"],
W=["* ", # W
"** ",
" **"],
X=[" * ", # X
"***",
" * "],
Y=[" * ", # Y
"****"],
Z=["** ", # Z
" * ",
" **"]
)
def plot_pentominos(pentominos):
fig, ax = plt.subplots()
ax.set_aspect('equal')
rectangles = []
for i, (name, block) in enumerate(pentominos.items()):
r, c = np.where(block == '*')
dx, dy = i % 4 * 6, i // 4 * 4
for x, y in zip(c + dx, r + dy):
rectangles.append(plt.Rectangle((x, y), 1, 1, facecolor=tab20.colors[i], edgecolor="white"))
# ax.text(dx + 1, dy - 1, name)
collection = PatchCollection(rectangles, match_original=True)
ax.add_collection(collection)
ax.autoscale_view()
ax.axis('off')
def as_array(b):
return np.array([list(row) for row in b])
pentominos_arr = {key:as_array(val) for key, val in pentominos.items()}
plot_pentominos(pentominos_arr)

ペントミノは、2次元のNumPy文字配列として表します。* はブロックがあることを示し、 (空白)はブロックがないことを示します。
pentominos_arr['W']
array([['*', ' ', ' '],
['*', '*', ' '],
[' ', '*', '*']], dtype='<U1')
箱詰めを解くコード#
次の5種類の箱を定義します。箱はNumPyの2次元配列で表し、1 はブロックを配置できる箇所、0 は空白のままにしてよい箇所を示します。
board1 = np.ones((8, 8), dtype=np.uint8)
board1[3:5, 3:5] = 0
board2 = np.ones((3, 20), dtype=np.uint8)
board3 = np.ones((4, 15), dtype=np.uint8)
board4 = np.ones((5, 12), dtype=np.uint8)
board5 = np.ones((6, 10), dtype=np.uint8)
boards = [board1, board2, board3, board4, board5]
print(board1)
[[1 1 1 1 1 1 1 1]
[1 1 1 1 1 1 1 1]
[1 1 1 1 1 1 1 1]
[1 1 1 0 0 1 1 1]
[1 1 1 0 0 1 1 1]
[1 1 1 1 1 1 1 1]
[1 1 1 1 1 1 1 1]
[1 1 1 1 1 1 1 1]]
ペントミノの配置可能な場所#
次のコードでは、すべてのペントミノが配置可能な場所を算出します。
ペントミノは pentomino[:, ::step] を用いて左右反転し、さらに np.rot90(fliped_pentomino, r) を使用して 90° 回転を4回行うことで、合計8種類の状態を生成します。それらを board のすべての位置に試し、配置に成功した場合は、そのペントミノの番号と配置したマスの座標を記録します。
重複を除去するために set を用いて配置情報を保存し、最後に sorted() を使用してリストに変換します。
from itertools import product
from collections import defaultdict, namedtuple
Location = namedtuple('Location', 'pentomino cells')
def get_all_locations(pentominos, board):
ymax, xmax = board.shape
locations = set()
for i, pentomino in enumerate(pentominos):
for step in (1, -1): # 左右反転
flipped_pentomino = pentomino[:, ::step]
for r in range(4): # 90°回転を4回実行
rotated_tile = np.rot90(flipped_pentomino, r)
locy, locx = np.where(rotated_tile == "*")
for y, x in product(range(ymax), range(xmax)):
locy2 = locy + y
locx2 = locx + x
try:
if np.all(board[locy2, locx2] == 1): # 配置可能か確認
loc = tuple(sorted(zip(locy2.tolist(), locx2.tolist())))
locations.add(Location(i, loc))
except IndexError:
pass # 配置がボード外に出た場合はスキップ
return sorted(locations)
次のコードでは、0番のペントミノの最初の5つの配置場所を表示します。
locations = get_all_locations(pentominos_arr.values(), boards[0])
for i in range(5):
print(locations[i])
Location(pentomino=0, cells=((0, 0), (0, 1), (1, 1), (1, 2), (2, 1)))
Location(pentomino=0, cells=((0, 0), (1, 0), (1, 1), (1, 2), (2, 1)))
Location(pentomino=0, cells=((0, 1), (0, 2), (1, 0), (1, 1), (2, 1)))
Location(pentomino=0, cells=((0, 1), (0, 2), (1, 2), (1, 3), (2, 2)))
Location(pentomino=0, cells=((0, 1), (1, 0), (1, 1), (1, 2), (2, 0)))
解を求める#
次の solve_board() 関数を使用して、箱詰めパズルの解を求めます。まず、locations リストから次の2つの辞書を作成します。
pentomino_locations:各ペントミノに対して、配置可能な場所のインデックスを対応付けた辞書。cell_locations:各マスに対して、そのマスを含む配置のインデックスを対応付けた辞書。
さらに、locations のすべての要素に対応するブール変数 flags を作成します。flags の値が True の場合、その Location は有効であることを意味します。
これらの pentomino_locations と cell_locations に基づき、次の2つの制約条件を設定します。
ペントミノの使用回数の制約(
pentomino_locations)各ペントミノは1回だけ使用できるようにします。
マスの充填制約(
cell_locations)各マスは1つのペントミノでのみ埋めることができます。
この制約を model.add_exactly_one()を用いて設定し、最適な解を求めます。
def solve_board(board):
locations = get_all_locations(pentominos_arr.values(), board)
# pentomino -> location index
pentomino_locations = defaultdict(list)
# cell_id -> location index
cell_locations = defaultdict(list)
for idx, (tile_id, location) in enumerate(locations):
pentomino_locations[tile_id].append(idx)
for loc in location:
cell_locations[loc].append(idx)
model = cp_model.CpModel()
flags = np.array([model.new_bool_var("b{}".format(i)) for i in range(len(locations))])
for d in (pentomino_locations, cell_locations):
for index in d.values():
selected_flags = flags[index].tolist()
model.add_exactly_one(selected_flags)
solver = cp_model.CpSolver()
solver.solve(model)
return [locations[i][1] for i, flag in enumerate(flags) if solver.value(flag)]
def plot_solution(solution):
h, w = np.array(solution).reshape(-1, 2).max(axis=0) + 1
fig, ax = plt.subplots(figsize=(w * 0.25, h * 0.25))
ax.set_aspect('equal')
rectangles = []
for i, block in enumerate(solution):
for y, x in block:
rect = plt.Rectangle((x, y), 1, 1, facecolor=tab20.colors[i],edgecolor='white')
rectangles.append(rect)
collection = PatchCollection(rectangles, match_original=True)
ax.add_collection(collection)
ax.autoscale_view()
ax.invert_yaxis()
ax.axis('off')
return fig
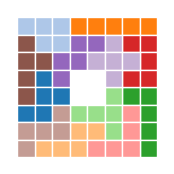
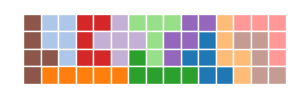
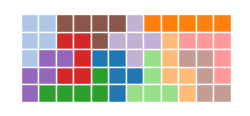
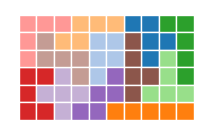
次に、すべての箱についてsolve_board()を実行し、それぞれの解を求め、グラフにします。
for board in boards:
solution = solve_board(board)
plot_solution(solution)