数独ソルバー#
本章では、数独ソルバーを例にして、充足可能性問題について説明します。
充足可能性問題#
充足可能性は、与えられたブール方程式を解き、問題を満たす変数の割り当てを見つけるために使用されます。ブール充足可能性問題(以下、SAT)は決定問題に属し、最初にNP完全であることが証明された問題です。これは、計算機科学の基礎理論、アルゴリズム、人工知能、ハードウェア設計など、多くの分野で重要な問題です。本章では、pysat を使用して数独ゲームを解く方法を紹介します。
まず、例を通じてブール方程式とは何かを説明し、それをSATソルバーが必要とする合取標準形(CNF) に変換する方法、そして pysat を用いた解法を紹介します。
論理推理問題
4人の容疑者が以下のように供述しました:
甲:「私が犯人ではない」
乙:「丁が犯人だ」
丙:「乙が犯人だ」
丁:「乙は私を陥れようとしている」
4人のうち、真実を話しているのは1人だけである。犯人を推理せよ。
4人の容疑者甲(A)、乙(B)、丙(C)、丁(D)について、それぞれが犯人であるかどうかをブール変数で表します。
例えば、A は「甲が犯人であること」を意味し、~A は「甲が犯人ではないこと」を意味します。
このとき、4人の供述は以下のようにブール方程式に変換されます:
容疑者 |
供述 |
ブール式 |
|---|---|---|
甲 |
私が犯人ではない |
S1 = ~A |
乙 |
丁が犯人だ |
S2 = D |
丙 |
乙が犯人だ |
S3 = B |
丁 |
乙は私を陥れようとしている |
S4 = ~D |
4人のうち1人だけが真実を話しているため、次の4通りのいずれかが成り立ちます(& は論理積, | は論理和):
S1 & ~S2 & ~S3 & ~S4 |
~S1 & S2 & ~S3 & ~S4 |
~S1 & ~S2 & S3 & ~S4 |
~S1 & ~S2 & ~S3 & S4
上記の式では、各行の式は論理積(AND)で結合され、行ごとは論理和(OR)で結ばれています。このような形式の論理式は 析取標準形(DNF)と呼ばれます。しかし、SATソルバーは合取標準形(CNF)でしか解くことができません。CNFとは、「複数の論理和(OR)で構成された節を論理積(AND)で結んだもの」です。したがって、次のように条件を変形して、「S1、S2、S3、S4 のうち 1 つだけが真である」ことを表します:
~(S1 & S2) &
~(S1 & S3) &
~(S1 & S4) &
~(S2 & S3) &
~(S2 & S4) &
~(S3 & S4) &
~(~S1 & ~S2 & ~S3 & ~S4)
この式では、S1、S2、S3、S4 の2つが同時に真である可能性を排除し、最後の ~(~S1 & ~S2 & ~S3 & ~S4) により、4つ全てが偽であることも排除しています。次に、ド・モルガンの法則(~(A & B) = ~A | ~B)を適用し、CNF に変換します。
変換結果(S1, S2, S3, S4 → A, B, C, D)
~S1 | ~S2 → A | ~D
~S1 | ~S3 → A | ~B
~S1 | ~S4 → A | D
~S2 | ~S3 → ~D | ~B
~S2 | ~S4 → ~D | D
~S3 | ~S4 → ~B | D
S1 | S2 | S3 | S4 → ~A | D | B | ~D
DNFからCNFに変換#
DNF(析取標準形)をCNF(合取標準形)に変換するのは手作業では煩雑ですが、SymPyを利用すれば、自動的に変換できます。
以下の手順で変換を行います:
❶ 変数の定義:A, B, C, D の 4 つのシンボルを定義する。
❷ DNFの作成:ビット演算子を使用して、問題の DNF 式を構築する。
❸ CNFへの変換:to_cnf() 関数を用いて、DNF を CNF に変換する。
❹ 化簡オプション:simplify=True を指定すると、式が簡略化され、直接問題の解が得られる。
from sympy import symbols
from sympy.logic.boolalg import to_cnf
A, B, C, D = symbols("A:D") #❶
S1 = ~A
S2 = D
S3 = B
S4 = ~D
dnf = ((S1 & ~S2 & ~S3 & ~S4) | #❷
(~S1 & S2 & ~S3 & ~S4) |
(~S1 & ~S2 & S3 & ~S4) |
(~S1 & ~S2 & ~S3 & S4))
cnf_1 = to_cnf(dnf, simplify=False) #❸
cnf_2 = to_cnf(dnf, simplify=True) #❹
cnf_2
satisfiable()を使用すると、論理式の推論を行うことができます。以下の結果は、論理変数Aが真であることを示しており、つまり甲が犯人であることを意味します。
from sympy.logic.inference import satisfiable
satisfiable(cnf_1)
{A: True, B: False, D: False}
以下に pysat ライブラリを使用して、この論理問題を解く方法を示します。CNF 公式は、ネストされたリストで表現できます。リスト内の各整数はブール変数に対応し、負の数は論理否定を示します。例えば、1 は A に対応し、1 は A を意味し、-1 は ~A を意味します。
❶ append_formula() を呼び出して、ネストされたリストで表現された CNF 公式をソルバーに追加します。複数回 append_formula() を呼び出して、さらに多くの式を追加できます。
❷ solve() を呼び出して、解を求めます。
❸ get_model() を呼び出して、解のリストを取得します。リスト内の各要素はブール変数に対応し、1 はその変数が真であることを示し、-1 は偽であることを示します。
結果から、甲が犯人であることがわかります。
from pysat.solvers import Solver
sat = Solver()
problem = [[1, -4], [1, -2], [1, 4], [-4, -2],
[-4, 4], [-2, 4], [-1, 4, 2, -4]]
sat.append_formula(problem) #❶
print(sat.solve()) #❷
print(sat.get_model()) #❸
True
[1, -2, -3, -4]
数独ゲーム#
数独は数字を埋めるゲームであり、プレイヤーは1から9までの数字を各マスに記入し、各行・各列・各ブロック(3×3の領域)に1から9のすべての数字が含まれるようにしなければなりません。次のグラフに示すように、黒い数字はゲーム作成者が提供したもので、これによりパズルの解が一意に決まります。灰色の数字はそのゲームの解答を示しています。
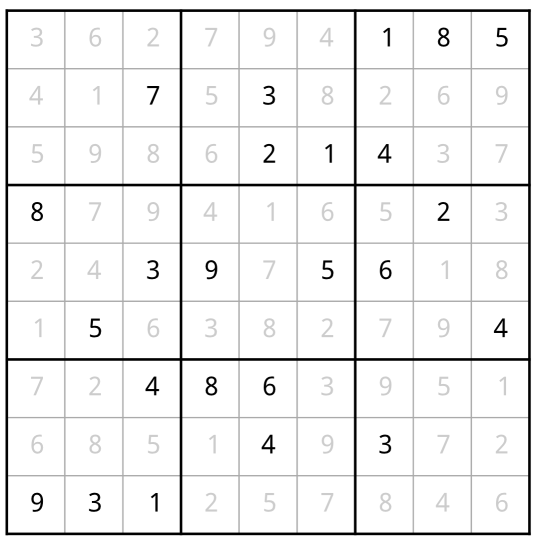
SATはブール論理を解くソルバーであり、各変数はFalseまたはTrueの2つの値しか取りません。数独のグリッドを表現するために、三次元配列 bools を使用します。その0番目の軸は数独グリッドの行、1番目の軸は列、2番目の軸は各セルの候補数字に対応します。例えば、最終的な解で bools[4, 1, 3] に対応するブール変数が真である場合、それは数独グリッドの5行目・2列目の値が4であることを意味します。なお、数独のゲームでは行・列・数字は1から始まりますが、プログラム内の配列のインデックスは0から始まることに注意してください。
以下の bools 配列には、SATソルバーで使用するブール変数の番号が保存されています。なお、SATのブール変数の番号は1から始まります。
import numpy as np
bools = np.arange(1, 9 * 9 * 9 + 1).reshape(9, 9, 9)
数独の制約条件に基づくと、以下のルールが成り立ちます:
各セルには1つの数字のみを記入可能
すなわち、boolsの第2軸(数字の候補)のブール変数のうち、各セルにつき1つだけがTrueとなる。各行に同じ数字は1つだけ存在可能
boolsの第1軸(列)の中で、各行において同じ数字のブール変数がTrueになるのは1つだけ。 例えば、bools[0, :, 2]は1行目の各セルにおける「数字3」のブール変数を表すが、1行には必ず1つの「3」しか存在できないため、この配列内でTrueになるのは1つだけ。各列に同じ数字は1つだけ存在可能
boolsの第0軸(行)の中で、各列において同じ数字のブール変数がTrueになるのは1つだけ。各ブロックに同じ数字は1つだけ存在可能
これについてはやや複雑で、boolsのインデックスを適切に調整する必要があるため、後ほど詳しく説明する。
数独の制約は、「ブール変数を異なるグループに分け、それぞれのグループ内で True になる変数が1つだけになるようにする」こと。では、SATを使って、この「グループ内で1つだけが True」という制約をどのように表現するかを見ていきます。
SATはCNFを使用し、各式はブール変数を「OR(論理和 |)」でつなぎ、式同士を「AND(論理積 &)」で接続します。我々が必要とするのは、「あるグループ内のブール変数のうち1つだけが True」という論理式です。
例えば、ブール変数 A、B、C の3つの変数について、この制約を満たすには以下の2つの論理式を組み合わせます:
少なくとも1つは
Trueであること: \(A | B | C\)2つ以上の変数が
Trueにならないこと: \(\neg(A \& B) \& \neg(A \& C) \& \neg(B \& C)\)
これは、「任意の2つの変数が同時に True にならない」ことを意味します。この条件は、ド・モルガンの法則を適用すると次のように変形できます:
つまり、次のSATの論理式を得ます:
上記の条件を数独の各制約に適用するには、N個の要素から2つの要素をすべての組み合わせで選び出す必要があります。これは Python の itertools.combinations を用いて実装できます。以下の get_conditions() 関数は、bools の最終軸にあるすべてのブール変数のうち、「1つだけが True になる」ことを保証するSATの制約を生成します。
❶ N個の要素から2つの要素を選ぶすべての組み合わせを作成
→ 2次元配列 index を作り、形状 (N * (N-1) / 2, 2) のペアを格納。
❷ 最初の条件(少なくとも1つが True)を表す論理式を生成
→ 各グループの論理変数の番号をORでつなぐ。
❸ 2つ以上の変数が True にならない制約を生成
→ 各組み合わせに対して、(~A | ~B) の形の制約を作成。
こうして、数独の制約を満たすSATの論理式を構築できます。
from itertools import combinations
def get_conditions(bools):
conditions = []
n = bools.shape[-1]
index = np.array(list(combinations(range(n), 2))) # ❶
# 最終軸をグループ化
# 条件1: 各グループで1つだけが真である
conditions.extend(bools.reshape(-1, n).tolist()) # ❷
# 条件2: 各グループ内で2つの値が同時に真にならない
conditions.extend((-bools[..., index].reshape(-1, 2)).tolist()) # ❸
return conditions
以下は、1、2、3 と 4、5、6 の 2 つの論理変数グループに対する演算結果です。
get_conditions(np.array([[1, 2, 3], [4, 5, 6]]))
[[1, 2, 3],
[4, 5, 6],
[-1, -2],
[-1, -3],
[-2, -3],
[-4, -5],
[-4, -6],
[-5, -6]]
以下では、get_conditions() を使用して数独の最初の3つの制約条件を計算します。これは最終軸に対してのみ演算を行うため、「各行の数字が重複しない」と「各列の数字が重複しない」という2つの条件については、対応する軸を最終軸に入れ替える必要があります。
c1 = get_conditions(bools) # 各セルには1~9のうち1つの数字のみを取る
c2 = get_conditions(np.swapaxes(bools, 1, 2)) # 各行で同じ数字は重複しない
c3 = get_conditions(np.swapaxes(bools, 0, 2)) # 各列で同じ数字は重複しない
制約条件4については、各ブロックのブール変数を最終軸に入れ替える必要があります。これには、reshape() と swapaxes() を交互に使用します。最後に、c1、c2、c3、c4 を連結してリスト conditions を作成すると、数独ゲームのすべての制約条件を満たすSATの論理式が得られます。
tmp = np.swapaxes(bools.reshape(3, 3, 3, 3, 9), 1, 2).reshape(9, 9, 9)
c4 = get_conditions(np.swapaxes(tmp, 1, 2)) # 各ブロック内で同じ数字は重複しない
conditions = c1 + c2 + c3 + c4
最後に、pysatを使用して数独ゲームを解きます。
❶ Solver.get_model() メソッドはリストを返すため、まずそれを (9, 9, 9) の形状に復元します。
❷ 次に、その配列の最終軸で正数に対応するインデックスを見つけ、実際に記入する数字はそのインデックスに 1 を加えたものになります。
プログラムの出力を注意深く観察し、数独の制約条件を満たしているか分析してください。
def format_solution(solution):
solution = np.array(solution).reshape(9, 9, 9) # ❶
return (np.where(solution > 0)[2] + 1).reshape(9, 9) # ❷
sat = Solver()
sat.append_formula(conditions)
print(sat.solve())
solution = sat.get_model()
format_solution(solution)
True
array([[2, 4, 6, 1, 3, 5, 8, 7, 9],
[1, 3, 5, 7, 8, 9, 2, 4, 6],
[8, 7, 9, 2, 4, 6, 1, 3, 5],
[5, 6, 3, 4, 1, 2, 7, 9, 8],
[4, 1, 2, 9, 7, 8, 5, 6, 3],
[7, 9, 8, 5, 6, 3, 4, 1, 2],
[6, 5, 4, 3, 2, 1, 9, 8, 7],
[3, 2, 1, 8, 9, 7, 6, 5, 4],
[9, 8, 7, 6, 5, 4, 3, 2, 1]], dtype=int64)
以下では、conditions を使用して実際の数独ゲームを解きます。ゲームの初期状態は sudoku_str によって指定され、0 は数字を記入する必要がある空白セルを表します。
❶ 初期状態の各非0の数字に対して、それに対応するブール変数が真であるというブール式を作成し、conditions2 を得ます。
❷ このゲームの解は、conditions と conditions2 の両方の条件を満たします。
sudoku_str = """
000000185
007030000
000021400
800000020
003905600
050000004
004860000
000040300
931000000"""
sudoku = np.array([[int(x) for x in line]
for line in sudoku_str.strip().split()])
r, c = np.where(sudoku != 0)
v = sudoku[r, c] - 1
conditions2 = [[int(x)] for x in bools[r, c, v]] # ❶
sat = Solver()
sat.append_formula(conditions + conditions2) # ❷
sat.solve()
solution = sat.get_model()
format_solution(solution)
array([[3, 6, 2, 7, 9, 4, 1, 8, 5],
[4, 1, 7, 5, 3, 8, 2, 6, 9],
[5, 9, 8, 6, 2, 1, 4, 3, 7],
[8, 7, 9, 4, 1, 6, 5, 2, 3],
[2, 4, 3, 9, 7, 5, 6, 1, 8],
[1, 5, 6, 3, 8, 2, 7, 9, 4],
[7, 2, 4, 8, 6, 3, 9, 5, 1],
[6, 8, 5, 1, 4, 9, 3, 7, 2],
[9, 3, 1, 2, 5, 7, 8, 4, 6]], dtype=int64)
conditions2 の各 OR 式には1つのブール変数しか含まれていないことに注目してください。このような単純な式には、assumptions パラメータを使って仮定条件を追加できます。この方法では、conditions の中の節だけを Solver に追加し、既知の真であるブール変数のリストを solver() メソッドの assumptions パラメータに渡します。assumptions を使用する利点の一つは、解決が完了した後、すべての仮定条件がクリアされることです。そのため、同じ sat オブジェクトを繰り返し使用して複数の数独ゲームを解くことができます。
sat = Solver()
sat.append_formula(conditions)
sat.solve(assumptions=bools[r, c, v].tolist())
solution = sat.get_model()
format_solution(solution)
array([[3, 6, 2, 7, 9, 4, 1, 8, 5],
[4, 1, 7, 5, 3, 8, 2, 6, 9],
[5, 9, 8, 6, 2, 1, 4, 3, 7],
[8, 7, 9, 4, 1, 6, 5, 2, 3],
[2, 4, 3, 9, 7, 5, 6, 1, 8],
[1, 5, 6, 3, 8, 2, 7, 9, 4],
[7, 2, 4, 8, 6, 3, 9, 5, 1],
[6, 8, 5, 1, 4, 9, 3, 7, 2],
[9, 3, 1, 2, 5, 7, 8, 4, 6]], dtype=int64)